The Lovasz number for random graphs (problems 17 and 18)

For a graph $G = (V, E)$, the clique number $\omega(G)$ and the chromatic number $\chi(G)$ are fundamental properties studied in combinatorics and graph theory. It is known that computing these quantities is, in general, NP-hard. However, in certain cases, it is possible to efficiently provide upper and lower bounds. As an example, for a $d$-regular graph $G$, it holds that $\chi(G) \leq d + 1$. In (Lovász, 1979), Lovász proposed a function $\vartheta(G)$, which was later named the Lovász number or the Lovász theta function, such that it can be efficiently computed and \begin{equation} \label{eq:lovasz_omega_chrom} \omega(G) \leq \vartheta(\overline{G}) \leq \chi(G), \end{equation} where $\overline{G}$ denotes the complement of the graph $G$.

The initial motivation of Lovász in (Lovász, 1979) was to bound the Shannon capacity of a graph. Consider the following setting: label the vertices of a graph $G$ with distinct letters, and say that two letters can be confused if their respective vertices are adjacent. Similarly, two sequences of length $k \geq 1$ can be confused, if for each $1 \leq i \leq k$, the vertices of the $i$-th letters are the same or adjacent. Let $m_k$ be the maximum number of sequences of length $k$, such that no two sequences can be confused. Clearly, $m_1 = \alpha(G)$, where $\alpha(G)$ is the independence number of $G$. The Shannon capacity of the graph $G$ is denoted by $\Theta(G)$ and is defined by \begin{equation} \Theta(G) := \lim_{k \to \infty} (m_k)^{1/k}. \end{equation} Surprisingly, even for simple graphs, such as the cycle on $7$ vertices $C_7$, the precise value of $\Theta(C_7)$ is unknown. The independence number and the Lovász number provide lower and upper bounds on the Shannon capacity, respectively:

\begin{equation} \alpha(G) \leq \Theta(G) \leq \vartheta(G). \end{equation}

In the following, we discuss how to bound the Lovász number for a certain family of graphs. Recall that the independence number, which is equal to the largest size of an independent set, can be defined as follows:

\begin{equation} \label{def:alpha} \alpha(G) := \max_{v \in \{0, 1\}^n} \Big\{\sum_{i} v_i \text{, such that } v_i v_j = 0\text{ for all }(i, j) \in E(G) \Big\}, \end{equation} where $E(G)$ is the set of edges.

Lovász number is a natural semidefinite programming (SDP) relaxation for Equation \ref{def:alpha}:

\begin{equation} \label{def:ltn} \vartheta(G) := \max_{X \in \mathbb{R}^{n \times n}} \Big\{\sum_{i, j} X_{ij} \text{, such that } X \succeq 0, \mathrm{Tr}\,X = 1, \text{ and } X_{ij} = 0\text{ for all }(i, j) \in E(G)\Big\}. \end{equation}

An interesting question is to characterize the Lovász number for random graphs. A well-known family of random graphs is the Erdős–Rényi random graphs $G(n, p)$. Here, $n$ denotes the number of vertices, and $0 \leq p \leq 1$ is the probability parameter. To sample a graph from $G(n, p)$, for each pair of vertices $i \neq j \in [n]$, one adds an edge independently with probability $p$. The random graphs $G(n, p)$ are ubiquitous in mathematics; for instance, they are used in combinatorics to lower bound Ramsey numbers. There are several results on the Lovász number for Erdős–Rényi random graphs $G(n, p)$ (see (Juhász, 1982), (Coja-Oghlan, 2005), and (Arora & Bhaskara, 2011)). However, the precise asymptotics of the Lovász number for $G(n, 1/2)$ is still open.

Conjecture 17

Let $G$ be distributed as $G(n, 1/2)$. Then, \begin{equation} \mathbb{E} \vartheta(G) = (1 + o(1))\sqrt{n}. \end{equation}

Lovász number exhibit a beautiful property (Lovász, 1979): for any graph $G$, \begin{equation} \label{eq:lovasz_complement} \vartheta(G) \vartheta(\overline{G}) \geq n. \end{equation} Note the connection to the inequality $w(G)\chi(\overline{G}) \geq n$ via Equation \ref{eq:lovasz_omega_chrom}. For vertex-transitive graphs $G$, which include circulant graphs, Equation \ref{eq:lovasz_complement} holds with equality.

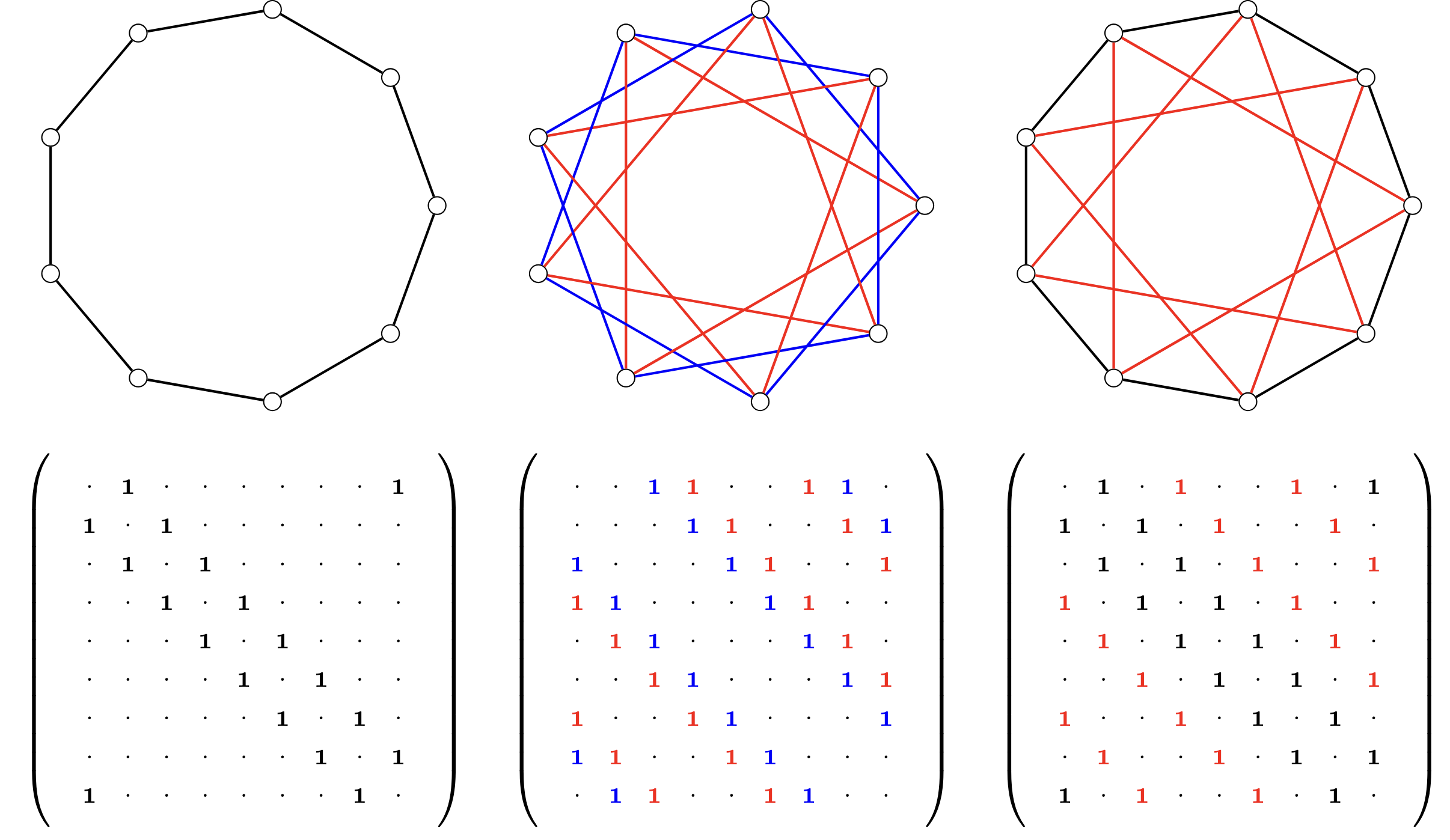Figure 1: Top row: Circulant graphs on 9 vertices;
Bottom row: Their corresponding adjacency matrices (with 0’s represented by dots).

Circulant graphs (see Figure 1) are examples of highly structured graphs and are defined as Cayley graphs over the cyclic group $\mathbb{Z}_n$. In other words, their adjacency matrix is circulant: if $(i, j) \in E(G)$, then $(i + 1\ \mathrm{mod}\ n, j+1\ \mathrm{mod}\ n) \in E(G)$. A celebrated example of a circulant graph from number theory is the Paley graph. For a prime $p \equiv 1\ \mathrm{mod}\ 4$, in order to define the Paley graph of order $p$, consider the vertex set $[p]$ and connect two vertices $i$ and $j$ if and only if $i - j$ is a quadratic residue modulo $p$. Paley graphs are of great importance in combinatorics and theoretical computer science, since they are believed to behave pseudorandomly: they are deterministic graphs which share certain properties with a typical realization of $G(p, 1/2)$. Current rigorous evidence of this phenomenon relies strongly on results from number theory and additive combinatorics.

Random (dense) circulant graphs can be viewed as a middle step between a ‘fully random’ $G(p, 1/2)$ and a ‘fully deterministic’ Paley graph. To sample a random circulant graph, we only need to sample the neighbors of a single vertex, say vertex $0$. Since $(0, k) \in E(G)$ implies that $(0, n - k) \in E(G)$, we sample a vector $x \in \{0, 1\}^{\left\lceil\frac{n - 1}{2}\right\rceil}$ uniformly at random, and $x_k = 1$ stands for $(0, k) \in E(G)$.

Table 1: Four equivalent LPs for $\vartheta(G)$.

’time’ domain

Primal	Dual
$$ \begin{aligned} \max_{x \in \mathbf{R}^n}\;&\sum_{i} x_i\\ \text{s.t.}\;& \begin{cases} x_k = x_{n - k}, & \forall k \in [n]\setminus\{0\},\\ x_0 = 1,\\ Fx \ge \mathbf{0},\\ x_k=0, & \forall (0,k)\in E(G). \end{cases} \end{aligned} $$	$$ \begin{aligned} \min_{z \in \mathbf{R}^n}\;&1 + \sum_i z_i\\ \text{s.t.}\;& \begin{cases} z_k = z_{n - k}, & \forall k \in [n]\setminus\{0\},\\ z \ge \mathbf{0},\\ \langle z, f_k \rangle = -1, & \forall (0,k)\in E(\overline G). \end{cases} \end{aligned} $$

‘frequency’ domain

Primal	Dual
$$ \begin{aligned} \max_{y \in \mathbf{R}^n}\;&n\,y_0\\ \text{s.t.}\;& \begin{cases} y_k = y_{n - k}, & \forall k \in [n]\setminus\{0\},\\ \lVert y \rVert_1 = 1,\\ y \ge \mathbf{0},\\ \langle y, f_k \rangle = 0, & \forall (0,k)\in E(G). \end{cases} \end{aligned} $$	$$ \begin{aligned} \min_{t \in \mathbf{R}^n}\;&1 + \,t_0\\ \text{s.t.}\;& \begin{cases} t_k = t_{n - k}, & \forall k \in [n]\setminus\{0\},\\ Ft \ge \mathbf{0},\\ t_k = -1, & \forall (0,k)\in E(\overline G). \end{cases} \end{aligned} $$

Let $F \in \mathbb{C}^{n \times n}$ be the discrete Fourier transform matrix: $F_{jk} = \exp(-2 \pi i jk/n)$ for $j, k \in [n]$. Here and in the following, we index vectors and matrices by $[n] := {0, 1, \ldots, n - 1}$. Let $f_k$ denote the $k$-th row of $F$. (Magsino et al., 2019) notes that, since circulant matrices are diagonalizable by $F$, the Lovász number for circulant graphs can be written as a linear program. In Table 1, we present four equivalent linear programs arising from strong duality (see, e.g., (Bazaraa et al., 2011)) and switching between the ‘time’ and the ‘frequency’ domains. For the latter, we perform the change of variables, $y := Fx$ and $t := Fz$, respectively.

We conjecture, based on numerical observations, that the Lovász number for random dense circulant graphs behaves similarly to that for $G(n, 1/2)$. This motivates the following question.

Conjecture 18

Let $G$ be distributed as a random dense circulant graph. Then, \begin{equation} \mathbb{E} \vartheta(G) = (1 + o(1))\sqrt{n}. \end{equation}

In (Bandeira et al., 2025), we provide a partial result towards resolving Conjecture 18, with a precise lower bound and an upper bound $O(\sqrt{n \log \log n})$. Our techniques rely on studying a modified version of a linear program from Table 1 in primal form and frequency domain, and using the restricted isometry property (RIP) of the subsampled discrete Fourier transform matrix.

References

1. Lovász, L. (1979). On the Shannon capacity of a graph. IEEE Transactions on Information Theory, 25(1), 1–7.
2. Juhász, F. (1982). The asymptotic behaviour of Lovász’theta function for random graphs. Combinatorica, 2(2), 153–155.
3. Coja-Oghlan, A. (2005). The Lovász number of random graphs. Combinatorics, Probability and Computing, 14(4), 439–465.
4. Arora, S., & Bhaskara, A. (2011). A note on the Lovász theta number of random graphs. Informal Note.
5. Magsino, M., Mixon, D. G., & Parshall, H. (2019). Linear programming bounds for cliques in Paley graphs. Wavelets and Sparsity XVIII, 11138, 440–447.
6. Bazaraa, M. S., Jarvis, J. J., & Sherali, H. D. (2011). Linear programming and network flows. John Wiley & Sons.
7. Bandeira, A. S., Błasiok, J., Dmitriev, D., Faure, U., Kireeva, A., & Kunisky, D. (2025). The Lovasz number of random circulant graphs. ArXiv Preprint ArXiv:2502.16227.