Fitting ellipsoids to random points (problem 6)

In this post I will discuss a seemingly simple question of high-dimensional stochastic geometry, which originated (as far as I know) in the series of works (Saunderson, 2011), (Saunderson et al., 2012), (Saunderson et al., 2013).

For $n, d \gg 1$, when can a sequence of $n$ i.i.d. random points in $\mathbb{R}^d$, drawn from $\mathcal{N}(0, \mathrm{I}_d/d)$, be fitted by the boundary of a centered ellipsoid?

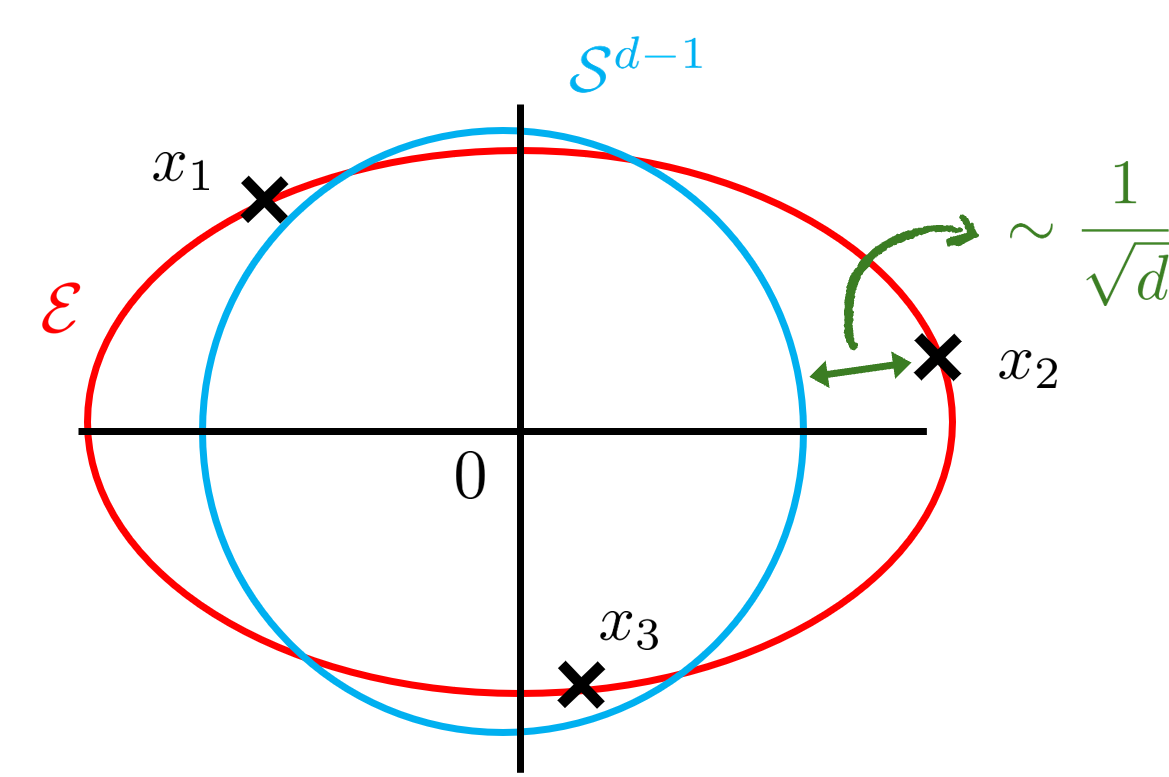Fitting Gaussian random points $x_i \sim \mathcal{N}(0, \mathrm{I}_d/d)$ to an ellipsoid. Notice that the unit sphere itself is close to being a fit by simple concentration of measure: a random $x \sim \mathcal{N}(0, \mathrm{I}_d/d)$ has (with high probability) distance $\mathcal{O}(1/\sqrt{d})$ to it.

The covariance being $\mathrm{I}_d / d$ is a convention which ensures $\mathbb{E}[|x_i|^2] = 1$: it is clear that assuming a generic positive-definite covariance $\Sigma \succ 0$ does not change this question, so we do not lose any generality with this assumption.

The motivation of (Saunderson, 2011), (Saunderson et al., 2012), (Saunderson et al., 2013) for this question came from statistics: they showed that the probability of existence of an ellipsoid fit was equal to the one of the success of a canonical convex relaxation (called Minimum-Trace Factor Analysis) in a problem of low-rank matrix decomposition. Several other motivations were uncovered later on, and I recommend reading the introduction of (Potechin et al., 2023) to learn more about them.

Interestingly, it was soon conjectured that a sharp transition occurs in the regime $n/d^2 \to \alpha > 0$, exactly at $\alpha = 1/4$, see e.g. Conjecture 2 of (Saunderson et al., 2013).

Conjecture 6 (Ellipsoid fitting)

Let $n, d \geq 1$ and $x_1, \cdots, x_n \sim \mathcal{N}(0,\mathrm{I}_d/d)$. For any $\varepsilon > 0$:
\begin{equation} \label{eq:ellipsoid_lower_bound} \limsup_{d \to \infty} \frac{n}{d^2} \leq \frac{1-\varepsilon}{4} \Rightarrow \lim_{d \to \infty} \mathbb{P}[\exists \mathcal{E} \textrm{ an ellipsoid fit to } (x_i)_{i=1}^n] = 1, \end{equation} \begin{equation} \label{eq:ellipsoid_upper_bound} \liminf_{d \to \infty} \frac{n}{d^2} \geq \frac{1+\varepsilon}{4} \Rightarrow \lim_{d \to \infty} \mathbb{P}[\exists \mathcal{E} \textrm{ an ellipsoid fit to } (x_i)_{i=1}^n] = 0. \end{equation}

Upper bounds

Ellipsoid fitting can be written as a semidefinite program (SDP), since any origin-centered ellipsoid satisfies $\mathcal{E} = \{x \in \mathbb{R}^d \, : \, x^T S x = 1\}$ for some positive semidefinite symmetric matrix $S$, so:

\[\begin{equation}\label{eq:ellipsoid_sdp} \mathbb{P}[\exists \mathcal{E} \textrm{ an ellipsoid fit to } (x_i)_{i=1}^n] = \mathbb{P}[\exists S \in \mathbb{R}^{d \times d} \, : \, S \succeq 0 \textrm{ and } x_i^T S x_i = 1 \textrm{ for all } i \in [n]]. \end{equation}\]

It’s then not hard to convince oneself that $\{x_i^T S x_i = 1 \}_{i=1}^n$ is an independent system of $n$ linear equations on $S$: this already gives an upper bound of $\binom{d+1}{2} \simeq d^2/2$ to the number of points that can admit an ellipsoid fit (with high probability). As of now, this ``silly’’ argument (which does not take into account the constraint that $S \succeq 0$) is the best upper bound established for Conjecture 6.

Lower bounds

On the other hand, there has been an abundance of works to establish lower bounds (Saunderson, 2011), (Saunderson et al., 2012), (Saunderson et al., 2013), (Kane & Diakonikolas, 2023), (Potechin et al., 2023), (Hsieh et al., 2023), (Tulsiani & Wu, 2023), (Bandeira et al., 2024). Not diving into details, they essentially all rely on carefully picking a candidate solution $S^\star$ to the linear system $\{x_i^T S x_i = 1 \}_{i=1}^n$ (e.g. the least Frobenius norm solution), and establishing that $S^\star \succeq 0$ for small enough $n$. The best results in this vein are due to (Tulsiani & Wu, 2023), (Hsieh et al., 2023), (Bandeira et al., 2024), which independently proved the following.

Theorem 7

Let $n, d \geq 1$ and $x_1, \cdots, x_n \sim \mathcal{N}(0,\mathrm{I}_d/d)$. There is $\delta > 0$ such that: \begin{equation} \nonumber \limsup_{d \to \infty} \frac{n}{d^2} \leq \delta \Rightarrow \lim_{d \to \infty} \mathbb{P}[\exists \mathcal{E} \textrm{ an ellipsoid fit to } (x_i)_{i=1}^n] = 1. \end{equation}

While it is not known if these methods can be pushed all the way to $\delta = 1/4$, it is conjectured that picking $S^\star$ as the minimal nuclear norm solution to the linear system $\{x_i^T S x_i = 1 \}_{i=1}^n$ gives this optimal value, and could be a path towards proving eq.\eqref{eq:ellipsoid_lower_bound}, see (Maillard & Kunisky, 2024).

The transition at $d^2/4$

Notice that the $d^2/4$ threshold can be uncovered both by numerical simulations (solving a SDP can be done efficiently), but also by a heuristic argument: if the linear equations $\{\textrm{Tr}[S x_i x_i^T] = 1\}_{i=1}^n$ were replaced by $\{\textrm{Tr}[S G_i] = 1\}_{i=1}^n$ with $G_i$ Gaussian i.i.d. matrices, the existence of a sharp transition would be a direct consequence of Gordon’s theorem (Gordon, 1988), and the value $d^2 / 4$ can even be recovered in this case as the squared Gaussian width of the cone of positive semidefinite matrices! While this heuristic was well-known, we formalized it in (Maillard & Bandeira, 2023), essentially by showing that the volume of the space of solutions is universal in both problems. We established from it the following sharp transition result.

Theorem 8 (Bandeira & Maillard (2023))

For any $\varepsilon, M > 0$, we define \begin{equation} \nonumber \mathrm{EFP}_{\varepsilon, M} \, : \, \exists S \in \mathbb{R}^{d \times d} \, : \, \, \mathrm{Sp}(S) \subseteq [0, M] \textrm{ and } \frac{1}{n} \sum_{i=1}^n |x_i^T S x_i - 1| \leq \frac{\varepsilon}{\sqrt{d}}. \end{equation} Notice that the original ellipsoid fitting problem of Conjecture 6 is $\mathrm{EFP}_{0, \infty}$. We prove: \begin{equation} \nonumber \limsup_{d \to \infty} \frac{n}{d^2} = \alpha < \frac{1}{4} \, \Rightarrow \, \exists M_{\alpha} > 0 \, : \, \forall \varepsilon > 0, \, \lim_{d \to \infty} \mathbb{P}[\mathrm{EFP}_{\varepsilon, M_{\alpha}}] = 1,
\end{equation} \begin{equation} \nonumber \liminf_{d \to \infty} \frac{n}{d^2} = \alpha > \frac{1}{4} \, \Rightarrow \, \exists \varepsilon_{\alpha} > 0 \, : \, \forall M > 0, \, \lim_{d \to \infty} \mathbb{P}[\mathrm{EFP}_{\varepsilon_{\alpha}, M}] = 0. \end{equation}

A few remarks are in order to clarify the conclusion of Theorem 8.

• The setting $\varepsilon \ll 1$ (but not going to $0$ with $d$) is precisely the regime where the problem is not trivially solved by the unit sphere (i.e. $S = \mathrm{I}_d$), since $(1/n) \sum_{i=1}^n |x_i^T x_i - 1| = \mathcal{O}(1/\sqrt{d})$ (cf. also the figure above).
• In the regime $n / d^2 < 1/4$, Theorem 8 shows that there exists ellipsoids which are: $(i)$ well-behaved (the spectral norm of $S$ is bounded), and $(ii)$ they fit the points $(x_i)$ up to an arbitrarily small error (but not going to $0$ with $d$).
• In the regime $n / d^2 > 1/4$, Theorem 8 rules out any well-behaved ellipsoid (i.e. with bounded spectral norm) as a possible fit, even allowing a small fitting error.

Theorem 8 provides the first mathematical result identifying a satisfiability transition in the ellipsoid fitting problem at the conjectured $d^2/4$ threshold. While we were not yet able to close Conjecture 6 from it, some parts seem tantalizingly close: e.g. the non-existence of ellipsoid fits for $n/d^2 > 1/4$ would now follow from showing that there is no ill-behaved ellipsoid fit (or that if there is an ill-behaved ellipsoid fit, there must also be a well-behaved one).

Other works

To keep this post at a reasonable length, I have not mentioned some other recent works which are in some way related to this problem, and to which I contributed (Maillard & Kunisky, 2024), (Maillard et al., 2024), (Erba et al., 2024). In (Maillard & Kunisky, 2024) we use non-rigorous tools that originate in statistical physics to extend the conjecture to other classes of random points beyond Gaussian distributions (and the conjectured satisfiability threshold can then be very different from $d^2/4$!), but also to study the typical geometrical shape of ellipsoid fits, and even to predict analytically the performance of the methods used to prove the lower bounds discussed above (cf. the conjecture on the minimal nuclear norm solution mentioned below Theorem 7).

Finally, in (Maillard & Kunisky, 2024) we realized that the ideas behind Theorem 8 can be adapted to problems in statistical learning: precisely, we characterize optimal learning from data in a model of so-called “extensive-width” neural network, a regime which is both particularly relevant in practical applications and which had so far largely resisted to theoretical analysis. In another recent preprint (Erba et al., 2024), we build upon these ideas to study a toy model of a transformer architecture.

References

1. Saunderson, J. J. F. (2011). Subspace identification via convex optimization [PhD thesis]. Massachusetts Institute of Technology.
2. Saunderson, J., Chandrasekaran, V., Parrilo, P. A., & Willsky, A. S. (2012). Diagonal and low-rank matrix decompositions, correlation matrices, and ellipsoid fitting. SIAM Journal on Matrix Analysis and Applications, 33(4), 1395–1416.
3. Saunderson, J., Parrilo, P. A., & Willsky, A. S. (2013). Diagonal and low-rank decompositions and fitting ellipsoids to random points. 52nd IEEE Conference on Decision and Control, 6031–6036.
4. Potechin, A., Turner, P. M., Venkat, P., & Wein, A. S. (2023). Near-optimal fitting of ellipsoids to random points. The Thirty Sixth Annual Conference on Learning Theory, 4235–4295.
5. Kane, D., & Diakonikolas, I. (2023). A nearly tight bound for fitting an ellipsoid to gaussian random points. The Thirty Sixth Annual Conference on Learning Theory, 3014–3028.
6. Hsieh, J.-T., Kothari, P., Potechin, A., & Xu, J. (2023). Ellipsoid Fitting Up to A Constant. International Colloquium on Automata, Languages and Programming, ICALP, 2023.
7. Tulsiani, M., & Wu, J. (2023). Ellipsoid fitting up to constant via empirical covariance estimation. ArXiv Preprint ArXiv:2307.10941.
8. Bandeira, A. S., Maillard, A., Mendelson, S., & Paquette, E. (2024). Fitting an ellipsoid to a quadratic number of random points. To Appear in Latin American Journal of Probability and Mathematical Statistics.
9. Maillard, A., & Kunisky, D. (2024). Fitting an ellipsoid to random points: predictions using the replica method. IEEE Transactions on Information Theory.
10. Gordon, Y. (1988). On Milman’s inequality and random subspaces which escape through a mesh in \mathbbR^n. Geometric Aspects of Functional Analysis: Israel Seminar (GAFA) 1986–87, 84–106.
11. Maillard, A., & Bandeira, A. S. (2023). Exact threshold for approximate ellipsoid fitting of random points. ArXiv Preprint ArXiv:2310.05787.
12. Maillard, A., Troiani, E., Martin, S., Krzakala, F., & Zdeborová, L. (2024). Bayes-optimal learning of an extensive-width neural network from quadratically many samples. ArXiv Preprint ArXiv:2408.03733.
13. Erba, V., Troiani, E., Biggio, L., Maillard, A., & Zdeborová, L. (2024). Bilinear Sequence Regression: A Model for Learning from Long Sequences of High-dimensional Tokens. ArXiv Preprint ArXiv:2410.18858.